This page is devoted to the following odd relationship between the Jones polynomial of a knot at -1 and the hyperbolic volume its complement. The point is to show the graphs from certain computer experiments.
First, look at all (approx 5000) alternating knots with exactly 13 crossing. Bellow is a plot of the volume of the complement vs. Pi * Log(JonesPoly(-1)).
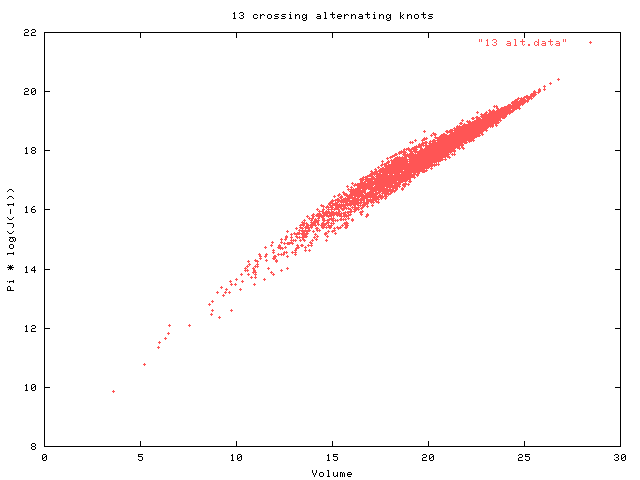
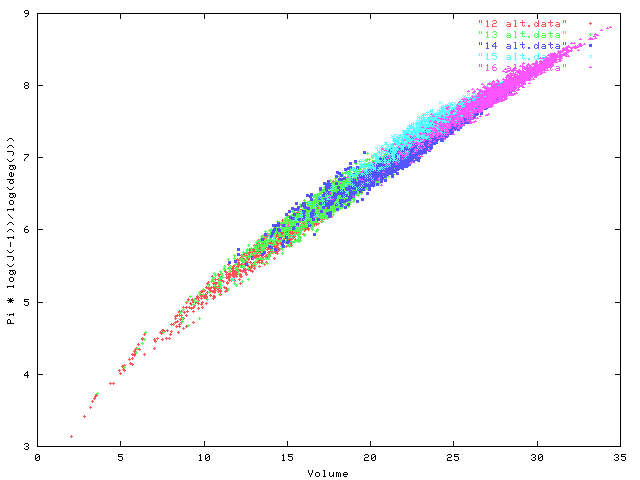
Notice the near linear relationship between these two quantities. It suggests that for alternating knots Log(JonesPoly(-1)) is almost a linear function of volume. A little thought shows that this can't be true, but that there might be a relationship of the form: log(J(-1)) is almost a linear function of Vol * log(deg(J)). In the next plot we examine the relationship for a) all alternating knots w/ <= 12 crossings (labled 12_alt), b) all alternating knots w/ 13 crossings, c) samples of alternating knots with 14, 15 and 16 crossings.
What about non-alternating knots? Well, these seem to lie "below" the alternating knots. The following two plots of the same data (on all knots with 13 or fewer crossings), but layered in different ways.
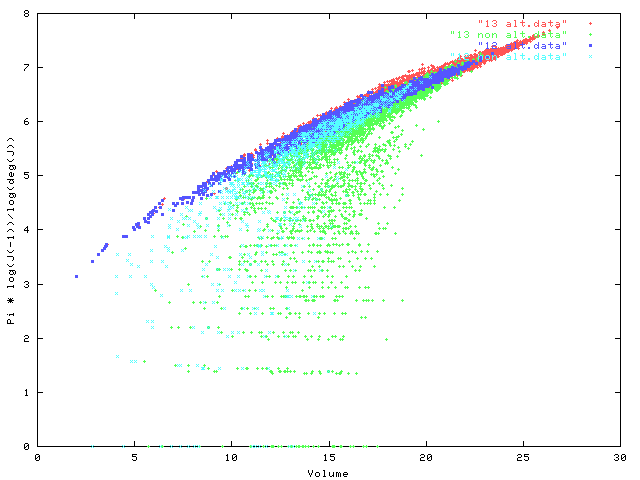
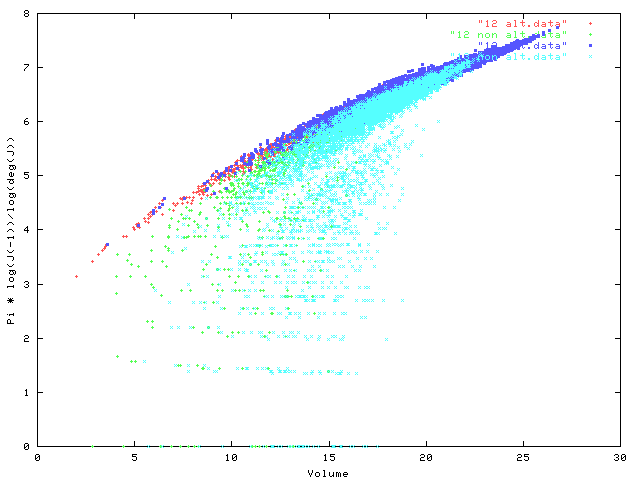
All of this suggests that there should be an inequality:
log(J(-1))/log(deg(J)) < a * Volume + b
Why?
Notes:
-Nathan